Puitar's Blog
0%

编译原理学习笔记2

Posted on Edited on In ,

词法语法分析基本概念

字母表

字母表（Alphabet）：字母表∑是一个有穷符号集合

  • 符号：字母、数字、标点符号、…

例如：

  • 二进制字母表：{0，1}
  • ASCII字符集
  • Unicode字符集

字母表的运算

  • 字母表$∑_1$和$∑_2$的乘积

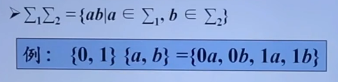
    image-20220706001340805

  • 字母表的n次幂

image-20220706001746142

  • 字母表的正闭包运算

image-20220706001834961

  • 字母表的克林闭包

image-20220706001936935

串

设∑是一个字母表，任意x∈∑*（克林闭包），x称为是∑上的一个串

由此可见，串是字母中符号的一个又穷序列

串s的长度，通常记为|s|，是指s中符号的个数

  • 例如|aab| = 3

空串是长度为0的串，用ε（epsilon）表示

  • |ε| = 0

串上的运算——连接

x和y是两个串，x和y的连接时把y附加到x的后面形成的串，记为xy

  • 例如x = dog且y = house，则xy = doghouse

空串时连接运算的单位元，即，对于任何串s有，εs = sε = s

image-20220706002929267

串上的运算——幂运算

image-20220706003037100

文法的定义

文法概述

image-20220706093506887

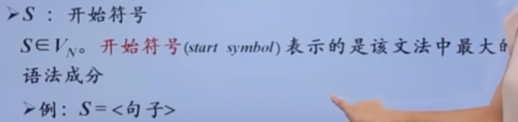
image-20220706093617730

image-20220706093821496

PS：E表示的是表达式

产生式的简写

image-20220706094045868

符号约定

image-20220706094125505

image-20220706094210869

image-20220706094418507

类型 示例 补充说明 示例
终结符 a,b,c 终结符号串 u,v,…,z
非终结符 A,B,C
文法符号 X,Y,Z 文法符号串 α,β,γ

语言的定义

推导和归约

image-20220707070400509

image-20220707070547641

推导和规约的例子

例句：little boy eats apple.

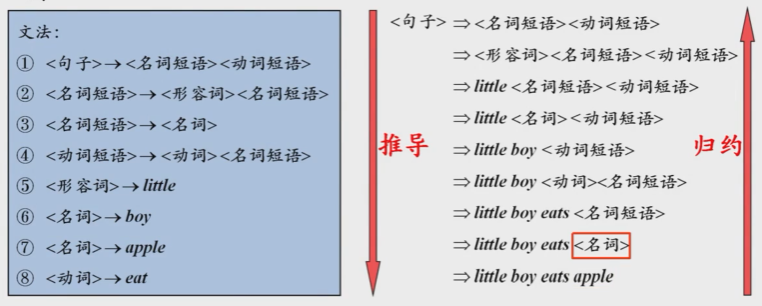
image-20220707070757275

句型和句子

image-20220707070943358

image-20220707071112194

可以产生无穷个句子，也就是说，文法解决了“无穷语言的有穷表达形式”。

文法定义标识符的例子

image-20220707071406429

课上提出的问题：请写出无符号整数和浮点数的文法定义

1
2
3
4
/* 无符号整数的文法定义 */
S->0|D(D∪0)*
D->1|2|3|...|9
PS: 无符号整数实际上就是0和非零数构成的，所以S由0和(D∪0)*[非零数]构成
1
2
3
4
5
6
7
/* 浮点数的文法定义 */
S->MFNE
N->.|ε	// 整数还是小数
M->+|-	// 符号
E->ED|ε // 任意长度的数字串或空串
F->FD|D // 非零长度数字串(浮点数非空)
D->0|1|...|9

文法的运算

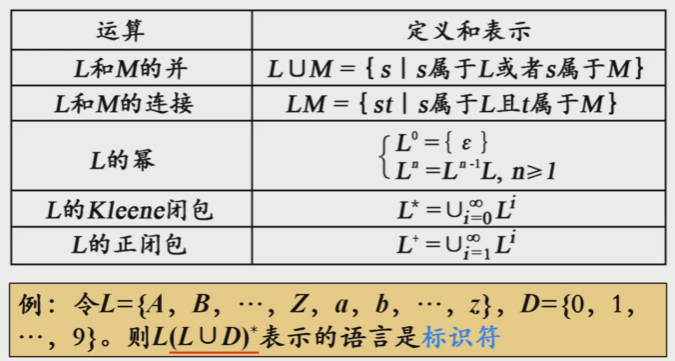
image-20220707074537980

文法的分类

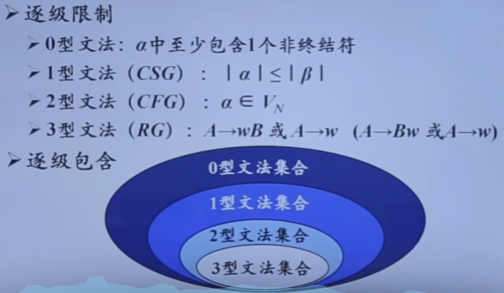
0型文法

image-20220707074702293

1型文法（上下文有关文法）

image-20220707074803369

2型文法（上下文无关文法）

image-20220707074916160

3型文法（正规文法）

image-20220707075219571

四种文法的关系

image-20220707075342222

判断文法类型
有文法G为：A->ε|aB，B->Ab|a，请判断文法G属于哪一类文法？
解题思路: 第一步：判断是否是0型文法，推导式左边是否至少包含一个非终结符，如果满足，则符合0型文法，；第二步：判断是否是1型文法：推导式右边的长度是否大于等于推导式左边的长度，如果满足，则符合1型文法；第三部：判断是否是2型文法，推导式左边是否是非终结符，如果满足，则符合2型文法；第四步：判断是左线性还是右线性，同时满足则不符合，只能是左线性和或者右线性中一个。
答案：2型文法

CFG的分析树

正则文法可以满足程序设计语言中的几乎所有单词构造，但是生成能力有限，不能满足句子构造。所以退而求其次，我们研究上下文无关文法的分析树。

分析树

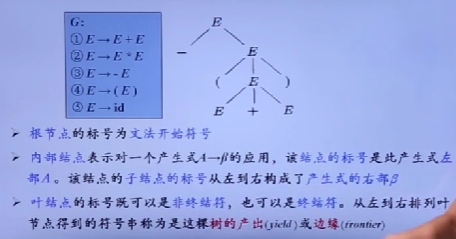
image-20220707075704552

分析树是推导的图形化表示！

image-20220707075918441

（句型的）短语

image-20220707080434612

  • 直接短语一定是某一个产生式的右部
    • 例如下面的“提高|人民|生活|水平”都是直接短语，都是④或者⑤的右部
  • 产生式的右部不一定是给定句型的直接短语
    • 例如“高人|民生|活水”，虽然是右部但是不是直接短语

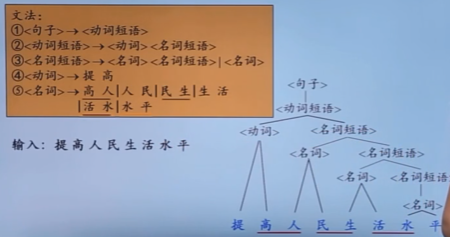
image-20220707080733037

这是由于，句型只是这个文法的一个特例模板，不一定式所有的右部的定义都用的上的。

二义性文法

如果一个文法可以为某个句子生成多棵分析树，则称这个文法是二义性的

让我们直接看一个例子，给定下面的文法和一个给定的句型，可以构造这个句型的两个分析树。

image-20220707081301716

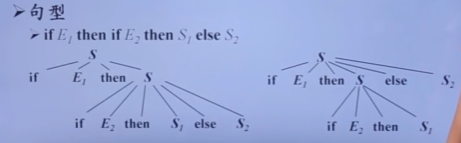
image-20220707081322485

由于这个文法可以为这个句型，构造两个分析树，所以称为二义性文法。大多数编译器都希望不要有二义性文法。因此要对文法进行改造，但是要付出代价，下面看看如何改造。

上面产生歧义的源头是：有两个if但是只有一个else！这使得else可以和两个if中的任意一个匹配。

大多数程序设计语言中都有这样的消歧规则：每一个else和最近的尚未匹配的if匹配。

因此引入这条规则上面两棵分析树只能保留左边的分析树。

image-20220707082156672